The NES game “Mike Tyson’s Punch-Out” uses a password system to allow players to continue from certain points in the game. Each password consists of 10 digits, each of which can be any number from 0 to 9. There are 2 kinds of passwords that the game will accept, which I’ll call “regular” and “special” passwords. Special passwords are specific sets of 10 digits that the game looks for and reacts to in a unique way when they are entered. The complete list of special passwords is as follows:

• 075 541 6113 – Busy signal sound 1
• 800 422 2602 – Busy signal sound 2
• 206 882 2040 – Busy signal sound 3
• 135 792 4680 – Play hidden circuit: “Another World Circuit” (must hold Select button and press A + B to accept password)
• 106 113 0120 – Shows credits (must hold Select button and press A + B to accept password)
• 007 373 5963 – Takes you to fight against Mike Tyson

The other kind of passwords that the game accepts are the regular passwords. Regular passwords are a coded representation of the progress that you’ve made in the game. The game data that is encoded into a regular password includes:

• Number of career wins
• Number of career losses
• Number of wins by knockout
• Next opponent to fight

Encoding Passwords

We’ll use an example game with 24 wins, 1 loss, 19 knockouts and starting at the world circuit title fight against Super Macho Man to see how passwords are generated.

The process of encoding this game state into a password begins by collecting your number of wins, losses and KOs into a buffer. The game represents each number in binary-coded decimal form with 8 bits per digit and 2 digits for each value. So for our 24 wins, that’s one byte with the value 2, and a second byte with the value 4. Then comes the pair of bytes for the number of losses and one more pair for KOs for a total of 6 bytes of data. The diagram below shows these 6 bytes with their values in both decimal and binary on the bottom.

The next step is to generate a checksum over those 6 bytes. The checksum byte is calculated by adding the 6 individual bytes together and then subtracting the result from 255. In our case we have 2 + 4 + 0 + 1 + 1 + 9 = 17 and then 255 – 17 = 238.

Next we shuffle some of the bits from the 6 bytes into a new buffer. We can think of the new buffer as a single 28-bit intermediate value that we’ll begin to fill in piece by piece. The bits from the first buffer are split into groups of 2 and moved around to different hard coded positions in the second. This is the first of a few steps whose sole job is to obfuscate the data make it difficult for players to see how passwords are generated.

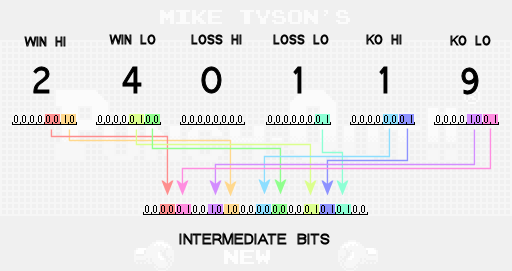
Notice that not all of the bits from the original buffer are transferred into the new intermediate buffer. These bits are ignored because they are known to always be 0. Your number of losses in particular only needs to contribute 2 bits of information to the password because of the rules of the game. If your total number of losses ever gets up to 3, you’ll get a game over and never get a password. Therefore, you only need to be able to represent the numbers 0, 1 and 2 for your number of losses and that requires only 2 bits.

Next we shuffle more bit pairs into the intermediate buffer. The first four pairs come from the checksum value that we computed earlier. The other pair of bits comes from the opponent value. The opponent value is a number that tells which opponent you’re going to fight next after you enter your password. There are three possible opponent values that can be used:

0 – DON FLAMENCO (first fight of major circuit)
1 – PISTON HONDA (first fight of world circuit)
2 – SUPER MACHO MAN (last fight of world circuit)

Since we wanted to generate a password that puts us at Super Macho Man, we’ll use 2 for our opponent value. The checksum and opponent value bits are then shuffled into the intermediate bits as follows:

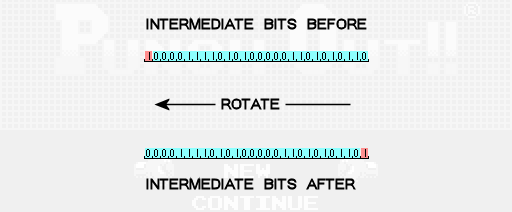
The next step is to perform some number of rotations to the left on the intermediate bits. A single leftward rotation means that all of the bits move one place to the left, and the bit that used to be the leftmost bit rotates all the way around to become the new rightmost bit. To calculate the number of times we’ll rotate the bits to the left, we take the sum of the opponent value and our number of losses, add 1, and take the remainder of that result divided by 3. In our case we have 2 + 1 + 1 = 4. Then the remainder of 4/3 is 1 so we’ll rotate the intermediate bits to the left 1 time.

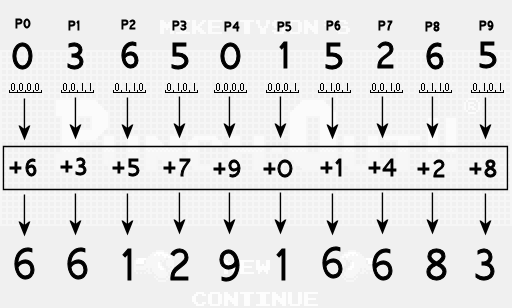
At this point the intermediate bits are thoroughly scrambled and now it’s time to start breaking them apart to come up with the digits that make up our password. Passwords need 10 digits so we’re going to break our 28 intermediate bits into 10 separate numbers that we’ll call password values P0, P1, P2, etc. The first nine password values will get 3 bits of data each, with the final value getting just 1 of the intermediate bits. To round out the final password value, we will also include bits that represent the number of rotations we performed in the previous step.

Finally we add a unique hard coded offset to the password value in each position. The final password digit is then the remainder of that sum divided by 10. For example in the seventh position we use an offset of 1, so we have 5 + 1 = 6, and then the final digit will be the remainder of 6/10 which is 6. In the fourth position the offset we use is 7, so we have 5 + 7 = 12, and then the final digit is the remainder of 12/10 which is 2.

Now we have the final password digits which we can try out in the game.

Decoding Passwords

The process of decoding a password back into the numbers of wins/losses/KOs and the opponent value is a straight forward reversal of all the steps outlined above and is left as an exercise for the reader. There are two notable mistakes however that the game makes when decoding and verifying player supplied passwords.

The first mistake happens in the very first step of decoding a password which would be to subtract out the offsets to get back to the password values. The original password values contained 3 bits of data each, which means their values before the offsets were applied must have all been in the range 0-7. However, a player might supply a password that results in a password value of 8 or 9 after the offset is subtracted out (modulo 10.) Instead of rejecting such a password immediately, the game fails to check for this case and instead allows the extra bit of data in the password value to pollute the collection of intermediate bits in such a way that passwords are no longer unique. Because certain intermediate bits could have either been set by the password digit that they correspond to OR the extra bit of a neighboring password value, there are multiple passwords that can now map back to the same set of intermediate bits. This is why you can find different passwords that give you the same in-game result, where as they would have been unique otherwise.

The second mistake is a bug in the logic the game uses to try to validate the data after decoding the password. The conditions that the game tries to enforce are:

• checksum that is stored in the password matches what the checksum should be given the win/loss/KO record stored in the password
• loss value is 0, 1 or 2
• opponent value is 0, 1, or 2
• rotate count stored in the password is the correct rotate count given the loss value and opponent value that were stored in the password
• all digits of win/loss/KO record stored in the password are in the range 0-9
• wins is >= 3
• wins is >= KOs

If any of these conditions are not met, the game intended to reject the password. However, there is a bug in the implementation of the final check (specifically when comparing BCD encoded numbers.) Instead of actually checking for wins >= KOs, the game will allow cases where the hi digit of wins is 0, the lo digit of wins is >= 3 and the hi digit of KOs is less than the lo digit of wins. For example, a record of 3 wins, 0 losses and 23 KOs will be accepted by the game (as demonstrated by the password 099 837 5823) when this was intended to be rejected (since you can’t have won 23 fights by knockout if you’ve only won 3 fights total.)

Conclusion

The particular details of this encoding scheme are unique to Punch-Out, but the general idea of taking some important bits of game state, transforming them in a reversible way to obfuscate their relationship to the original game state, and then using them to generate some number of symbols to show to the player as a password is fairly universal. Checksums can be used to make sure that accidental random changes to the password (if your finger slips while entering it) are most likely to result in an invalid password instead of some other password representing a random other game state.

If you’d like to offer feedback or keep track of when new posts in this series become available, you can follow me on twitter @allan_blomquist

(This is part 1 of a series – Next)

To round out my discussion of Contra I’m going to cover a few miscellaneous topics that don’t warrant a full writeup on their own. Some of these things are details of the game’s programming and some are just interesting things about the game itself that I never knew before. I’ll start off with a table of contents for this series for easy reference and then dive into the last few details.

Previous Posts about Contra

• Introduction
• Levels
• Random Enemies
• Base Enemies
• Collision Detection
• Player Control

Random Numbers

Contra has a single global 8-bit value that it uses as the source of randomness throughout the game. The way that it updates the random value each frame is kind of interesting in that it doesn’t implement any particular algorithm that you can call on once per frame to get the next number in the sequence. Instead, the next random value is generated by spinning in a tight loop during the time that the game is idle and waiting for the next display frame to begin (while waiting for the vblank interrupt.) During that time, the game continually adds the current frame counter value into the random number over and over again until the video hardware in the NES signals to the game that it’s time to begin processing for the next display frame. One consequence of this approach is that the particular sequence of random numbers you’ll get is heavily dependent on the exact cycle level operation of the CPU and the interaction between the CPU and the video hardware. That means that even if two emulators implement the logic of the CPU instructions perfectly, they will still generate different random sequences if their timing is not exact. You can see an obvious manifestation of this in the attract mode of Contra which plays back a pre-recorded stream of button input and relies on determinism to replay the demo exactly the same each time. Below is a side by side comparison of the same frame of the attract mode running on two different emulators. Notice that the running soldier that has randomly spawned on the lower right part of the screen selected a single spawn when running on Nintendulator and a triple spawn when running on NESten. This is because the sequence of random numbers being generated by the two instances of the game is not the same. Fortunately, the influence of the random numbers is small enough to not completely break the attract mode playback.

Structure of Arrays

Contra stores all of its data about enemies and bullets in structure-of-arrays format instead of the more object oriented array-of-structures format. The reason for this doesn’t have to do with CPU cache utilization or SIMD instructions like you might expect, but is instead a consequence of the NES having 16-bit memory addresses but only 8-bit CPU registers. If you want to access data indirectly through a pointer, you can’t store the address of the object in the pointer and then hard code the offset to the member you want in the load instruction because the address of the object probably won’t fit into a CPU register. Instead, you need to flip everything around and hard code the full 16-bit address of an array of members for multiple objects into your load instruction and then use the register to hold the offset within the array to get to the member that belongs to the object that you’re interested in.

Screen Space

In Contra, everything happen in screen space. The positions of the players and the positions of the enemies and bullets are all stored and manipulated within the coordinate system of the screen (i.e. a position of 0 always means the point in space that is currently at the left side of the screen, no matter where within the level the screen has scrolled to.) This is an optimization that seems a little counter intuitive at first because you would think that storing all of your positions in screen space would make things like scrolling a lot more complicated. Now instead of just changing a single scroll position variable to scroll the screen, you have to manually move the positions of every enemy, player and bullet every frame to simulate scrolling. The reason that this actually ends up being a good thing to do is that it saves a lot more time than it costs each frame. Scrolling is more complicated, but it really just boils down to adding 1 extra number into an object’s position as it updates each frame which is often just 1 extra CPU instruction per game object. The big win is that now all calculations related to the positions of things can be done using 8-bit values (the NES screen is 256×240 pixels so you can locate any position on screen with pixel precision using a single byte for X and Y.) Since the NES only supports 8-bit arithmetic natively this ends up being way faster than trying to emulate 16-bit arithmetic to handle 16-bit world positions. This of course only works for a game like Contra where the relationship between world space and screen space is a simple translation without any scaling or rotation possible (i.e. transforming from world to screen space happens to be commutative with other translations even though applying transforms is not commutative in general.) If the camera could zoom out in the game then things would start moving too fast and if the camera could rotate then things would go in the wrong direction.

Subtle Behavior

There are a number of things in Contra that change according to how many times you’ve played through the game in a single sitting, and which gun you currently have. The following is a complete list of the differences, where FINISHED would be 0 the first time through the game, 1 the second time through, etc. and GUN is 0 for your default weapon, 1 for Fire, 2 for Machine gun or Laser and 3 for Spread:

• Level 8 mid boss and final boss HP = 55 + (16 * FINISHED) + (16 * GUN)
• Level 8 mid boss projectile HP = 2 + FINISHED
• Level 8 mouth things in wall HP = 4 + (2 * FINISHED) + GUN
• Level 8 scorpions HP = 2 + FINISHED + GUN
• Level 8 pods around final boss HP = 24 + (2 * FINISHED) + (2 * GUN)
• Level 6 boss HP = 64 + (8 * GUN)
• Red cannons that comes up out of the ground wait less time to begin shooting at you for greater FINISHED
• Random enemy spawns are more frequent with greater FINISHED and GUN, and when FINISHED is 0 they take care not to spawn right on top of you and only spawn on the right side of the screen in the first level
• Gray turrets in walls rotate to target you faster, and wait less time to target again after shooting bullets with greater GUN
• Soldiers that shoot bullets tend to shoot more bullets per round with greater GUN
• Cannons on screen for level 2 and level 4 bosses, as well as the bosses themselves, wait less time between shooting at you for greater GUN
• Level 8 mid boss shoots 3 projectiles at a time when GUN is 3, but only 2 otherwise
• Speed at which scorpions drop down on you from the ceiling during final boss fight increases proportional to GUN

Conclusion

Contra is one of my favorite games on the NES and as a game programmer it was a lot of fun to dive in and figure out exactly how it works. I’m always amazed at how much game developers of the time were able to get out of hardware that is ridiculously slow and limited compared to today’s consoles. If you have any feedback about this series of posts please let me know so I can come up with a plan for if/when/what I’ll cover next. You can reach me on twitter @allan_blomquist or comment below.

(Prev – This is part 7 of a 7 part series)

Player Physics

The code that controls the low level player movement in Contra is very simple compared to what’s possible with a modern physics engine.  At the same time, I’ve always enjoyed the super responsive feel that a lot of older games have compared to games with more physically realistic controls. The data associated with low level motion in Contra is basically just a 2D position and velocity. Both are represented in 8.8 fixed point format with units of pixels, and pixels / frame respectively. Each frame, the game determines what the current velocity should be for a player and then simply adds that velocity into the player’s position. Horizontal velocity is always reset to 0 at the beginning of a frame so there is never any continuous acceleration in the X direction (so no ice physics are possible in Contra.)  Enemy characters in the game don’t even get their own dedicated memory to keep track of velocity because a lot of them don’t move. Those enemies that do move usually just manually add some constant amount to their current position each frame.  In the rare case that an enemy does need more complex movement, they implement their own version of what they need to do, not sharing any physics code with the player characters.

In general, there is no physics system that is always running to manage the movement of the players. Instead, certain calculations related to player movement are performed explicitly each frame depending on what exactly the player is doing at the time. For example, when the player is running along the ground, the play control code is setting the player’s horizontal velocity and checking for collisions at the player’s feet to see if you should start falling. However, the player’s vertical velocity is not being updated or even added into the player’s Y position at all.  Also, collisions are not being checked for above the player’s head because the player is known to not be moving up while running. This differs from the more general approach to physical simulation where gravity would be constantly pulling the player down into the ground and a reaction would be constantly moving the player back up to resolve the collision. Similarly, while jumping, collisions are only checked for above the player’s head while the player is moving up during the first part of the jump. Once the peak of the jump is reached and the player starts moving down, the code switches to checking for collisions below the player to see if you’ve landed yet. Also while jumping, vertical acceleration is applied by manually adding a fixed value into the player’s Y velocity each frame. There is no general acceleration variable that is always being added into the player’s velocity but that happens to only get a non-zero value during a jump. There are no wasted collision checks and no wasted math is performed to calculate the movement of the player. Only the relevant details are processed explicitly each frame and this contributes to a very tight feeling control scheme without much emergence of behavior.

Player States

At the next higher play control level above the low level physics code, it’s common to define a set of possible states that the player can be in and then update the player each frame according to the current state. Contra effectively implements this kind of system although it doesn’t actually use a single value to keep track of the current state of the player. Instead, players have multiple groups of flags that indicate what kind of state the player is currently in. The major groups are the jumping flags, falling flags and water flags. When the player is on the ground all of these flags are clear. If you press A to jump, the jumping flag is set and some other jump specific flags are updated according to which direction you’re trying to move and which direction you were facing when you left the ground. A similar set of flags exists for falling which is the state you go into when you run off the edge of a platform or jump down through the ground. The water flags are used only in the first level when you enter the water and start swimming. These flags are never used at the same time (i.e. you’ll never find both the jumping and falling flags set at the same time) so I’m not sure why a single state variable wasn’t used instead. It’s common for play control functions to start off by testing the various flags and then jumping off to specific parts of their code depending on which flag they find set.

Control Details

Running in Contra is instant on / instant off unlike some other games like Super Mario Bros. that impart the player character with some momentum. As mentioned earlier, this is a result of the horizontal velocity of the player being reset to zero at the start of each frame and then updated to the desired value depending on what the player is doing. If the player is running on the ground and you stop pressing left or right, then the horizontal velocity remains set to zero and the character instantly stops moving forward.

Jumping and falling have a slightly different behavior where once you start moving forward or backward, you will continue to move in that direction until you either collide with something or press the opposite direction to move the other way instead. Once you’re moving horizontally in the air, you aren’t able to stop moving horizontally until you land. This is similar to the spinning jump in Metroid and differs from games like Mega Man where you will stop moving in the air if you let go of your button input. Contra’s jump behavior is implemented by a pair of flags that are part of the jumping flags as described earlier. Pressing left or right during a jump will cause the corresponding left or right jump flag to turn on, but releasing the buttons does not cause the flags to turn off. Then, your horizontal velocity during a jump is set based on the current value of the flags and not directly from your current button input.

Contra also allows you to jump down through the ground to lower platforms by holding down on the controller and pressing the jump button. This same mechanic is also used in games like Chip ‘n Dale Rescue Rangers on the NES, but is absent from games with similar “one way” platforms (platforms that you can pass through while jumping up from below, but that you land on when falling down onto them) like Super Mario Bros. 2. In Contra, when you press A while holding down on the controller, the player’s falling flag is set instead of the jumping flag. In order to allow you to pass through the ground, the game records the location on screen that is 20 pixels (a little more than one full collision tile) below your current Y position. Then, as you fall down, the collision check that is normally performed at the player’s feet when in the falling state is skipped while the player’s current Y position is still above that recorded value.

Up Next

The next post will be the final installment in my series on Contra. I’ll cover a bunch of miscellaneous details that I think are interesting but don’t fit in anywhere else. If there’s anything that I haven’t covered so far that you’d like to know about how the game works let me know on twitter @allan_blomquist or leave a comment below!

(Prev – This is part 6 of a 7 part series – Next)

Collision Detection

There are two kinds of collisions that can happen in a game of Contra: object vs. object collisions, and object vs. level collisions. Each is handled by completely different code and detected using completely different data, so they are basically two separate systems.

Object vs. Object Collision

In the first post of this series, I mentioned that the game keeps track of three different kinds of objects: players, bullets from players, and enemies. Collision detection is one of the areas where this separation comes into play. Instead of checking for collisions between any and all of these objects, the game only checks collisions between the groups that will react to each other. Players never interact with other players or their bullets, and enemies never interact with other enemies, so the only collisions that matter are those between players and enemies, and those between player bullets and enemies.

Given that enemies are always involved in the object/object collisions that matter, collision detection between objects is done as part of updating all of the enemies. Each frame, the game loops over each active enemy and runs its particular update logic. After an enemy updates, the collision system kicks in and checks that enemy for collisions with players, and then collisions with player bullets. Each enemy has a pair of flags that can be used to indicate to the collision system whether either or both of these kinds of collisions are enabled for that enemy. This is how some enemies, like the bodies of turrets, are able to be shot by the player (by allowing collisions with player bullets) but not able kill you if you walk into them (by not allowing collisions with players.) Beyond these flags, no special logic is used to narrow down the list of potential collisions for an enemy. Every enemy is simply checked against every player and every bullet.

Checking for a collision between a given enemy and a given player is based on a point vs. rectangle test. The point that represents the player’s current position is checked against the rectangle that represents the current hit box that the enemy is using. If the point is inside the rectangle at the moment the check is performed then a collision has occurred. At first glance this seems a little strange. You need the player to be able to be shot in the head as well as the feet, but only the point that represents the player’s current position (which is usually fairly close the the center of the player sprite) is checked for collision with the enemy hit box. The key to making the system work is that the enemy hit boxes are not just tight bounds around the enemy sprites themselves, but rather representations of the area where collisions would occur if we were doing a more traditional rectangle vs. rectangle test. Put another way, the hit boxes that enemies use represent the space where the player position would have to be to make the player sprite overlap the enemy sprite.

You can see this process in action in the image above. In each of the three sections, the player’s position is indicated by a single green pixel in the center of a green circle. The pink rectangle represents the hit box that the white enemy bullet is using to check for collisions against the player’s position. Notice how the enemy bullet uses a different hit box depending on what the player is doing. This is how the game effectively changes where the player is vulnerable without actually having a hit box around the player to work with. Each enemy has a version of their hit box to use against a player in the water, a jumping player, a player on the ground, a standing/running player, and a player bullet. The particular type of player bullet is not taken into account when picking a hit box to test against so there is no difference between the different guns you can get from a bullet collision perspective.

Object vs. Level Collision

Collisions between objects and the level itself are not handled by a system in the way that collisions among objects are. Instead, level collisions are tested for directly wherever they are needed. If a player needs to know if he has run off the end of a platform then the code that updates a running player will query for a collision at the player’s feet every frame until it finds that there is nothing there. Most enemies don’t need to know about collisions with the level at all, but those that do will similarly check for them at specific times as needed. The only kind of query that is supported is checking a point against the level collision map that we’ve talked about before. The collision query returns the collision code for tile under the point that was checked (empty, solid, water or platform) and then the caller will do whatever it needs to in response to the different results.

3D Collision

Collisions in the pseudo-3D base levels work almost exactly the same as in the 2D levels but with certain constraints to make the effect hold up in fake 3D. Enemies are not allowed to collide with the player if their screen space Y position is too small (i.e. too far toward the top of the screen which means too far back “into” the screen.) This works because players are known to always be at the bottom of the screen during these levels. Player bullets are timed and only allowed to collide with most enemies once they have been on screen long enough to have reached the “back” of the room. For enemies that can be shot at any Z position within the room (like the rolling grenades that you have to blow up before they roll down and kill you) the timer on your bullets is not used. Instead, a flag is checked to see if your bullet was fired while you were lying on the ground, and if so, normal 2D collision detection is allowed to continue as usual. This works only because you are detecting a collision between two objects that are both known to be on the ground where Y position maps directly to Z position (i.e. if two things look like they are colliding in 2D, then you know they are colliding in 3D as well, but only along the ground.) With these constraints in place, the normal, flat 2D collision detection system can be used to detect collisions between objects even in a pseudo-3D environment.

(Prev – This is part 5 of a 7 part series – Next)

Static Base Enemies

The enemies in the pseudo-3D “base” levels in Contra are spawned by a slightly different system compared to the other kinds of levels. Base levels are also divided up into screens, and each screen also gets its own list of enemies that it needs to spawn, but the details of the list are different.

The screens in the base levels do not scroll, so each enemy in the screen enemy list is spawned the moment you enter the screen. Each enemy list starts off with a count of how many targets need to be destroyed on that screen in order to lower the electric barrier and allow you to move forward. The game actually has a bit of unused logic to lower the barrier right away if there are no targets even though there are no screens in the final game that are set up this way. The rest of the enemy list consists of a series of records for each enemy that needs to be spawned. The first piece of data in each record gives the X and Y position for where the enemy should spawn on screen. The second piece of data in each record gives the enemy type to spawn, and the third and final piece is an opaque creation context value just like the one in the enemy lists for the other kinds of levels.

At the moment that you enter a new screen, all of the enemies on that screen’s enemy list are spawned and the list is never referenced again. These enemies are mostly just the stationary things on the back wall like the targets and guns that shoot at you. All of the other enemies that run onto the screen while you’re playing are not spawned through the screen’s enemy list. Instead, they are handled by a different system.

Sequenced Base Enemies

One type of object that is a part of the enemy list for every screen in a base level isn’t actually a visible enemy, but an entity whose job it is to manage all of the enemies that run in from the sides of the screen as you play. This spawner entity processes its own completely separate enemy list for each screen that tells it which enemies to spawn and when. These enemy lists also contain a series of records, one for each enemy that needs to be spawned. The first piece of data in each record determines which kind of enemy to spawn and gives the creation context value for that enemy. The second piece of data gives a delay time to wait before spawning the next enemy. There is also a flag associated with each record that tells if that record is the final one for that screen. Once the final record has been processed, the spawner entity loops back to the first record and begins repeating the same pattern of enemies over and over. Once the whole pattern has been run through 7 times on a single screen, the spawner entity destroys itself so no more enemies will be spawned. This is what triggers the targets on the walls to begin shooting bullets at the player.

Power-up Enemies

On some of the screens in base levels you encounter a red jumping enemy that gives you a power-up when killed. The appearance of these enemies is mostly just specified by the secondary enemy list that the enemy spawner follows, but with the additional rules that only 1 of these red enemies can spawn on any given screen, and you can not spawn a red enemy during the first pass through the secondary enemy list. The creation context data for the jumping enemy in the spawner’s enemy list determines whether or not it can be one that carries a power-up, and if so, what kind of power-up it will drop when killed by the player. The 1 enemy per screen rule applies to spawning the enemy, not killing it, so if you miss the red enemy the first time you won’t get another one again on that screen.

(Prev – This is part 4 of a 7 part series – Next)